AVL Trees
Bringing balance to your life...
Nathan Tenney
WSU Tri-Cities
AVL Trees
- Methods for balancing
- Problems with these methods?
AVL Trees
- Build the concept of balancing into the tree itself
- These trees can be called "Self Balancing"
- AVL Trees
- Red/Black Trees
- Splay Trees
- Perform balancing during specific tree operations
AVL Trees
- Each node stores a "balance factor"
- Height of the right subtree minus the height of the left subtree
- The balance factor each node may differ only by 1 (-1, 0, 1).
- Does not guarantee a perfectly balanced tree (in comparison to the previous methods)
- If the balance factor for any node becomes > 1 or < -1 the tree needs to be rebalanced.
- Accomplished using rotations
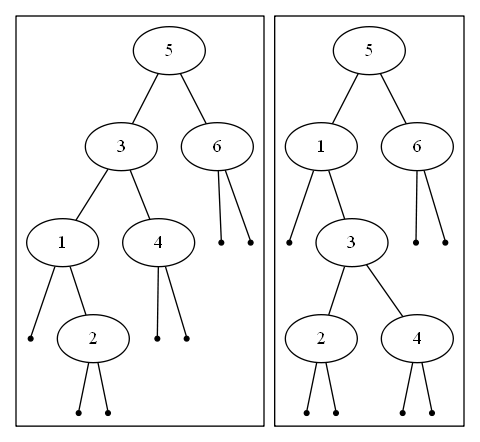
Balancing Trees: Right Rotation
- Node is a left child of parent
- Nodes parent becomes nodes right child
- If node had a right child, it becomes the left child of parent
- Node becomes the child of grandparent (either left or right, depending on where the parent was)
Balancing Trees: Right Rotation
Balancing Trees: Left Rotation
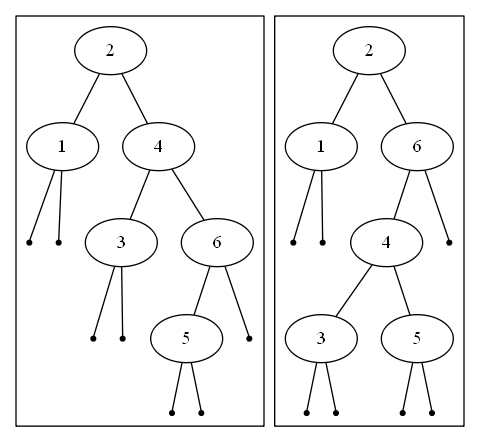
- Node is a right child of parent
- Nodes parent becomes the nodes left child
- If the node had a left child, it becomes the right child of parent
- Node becomes the child of grandparent (either left or right, depending on where the parent was)
Balancing Trees: Left Rotation
AVL Trees
AVL Trees
- Four conditions we need to be concerned about (only need to consider 2, the others are symmetrical).
- Insertion of a node into the left subtree of the left child (outside case)
- Insertion of a node into the left subtree of the right child (inside case)
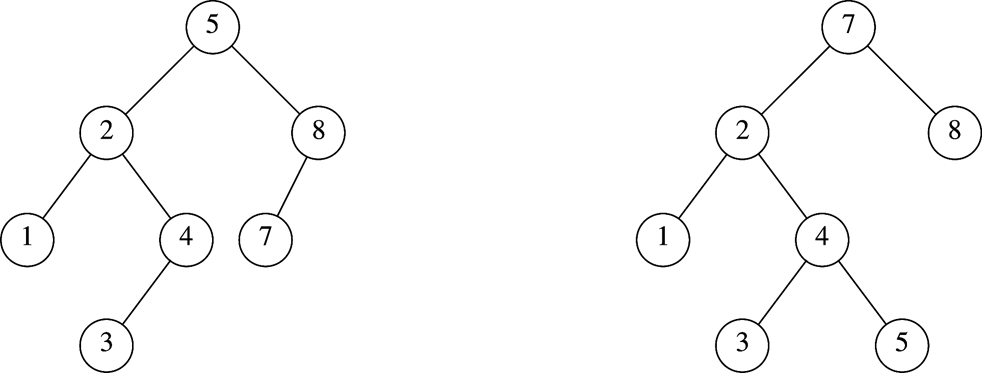
Left-Left case
- Can be fixed by a single rotation
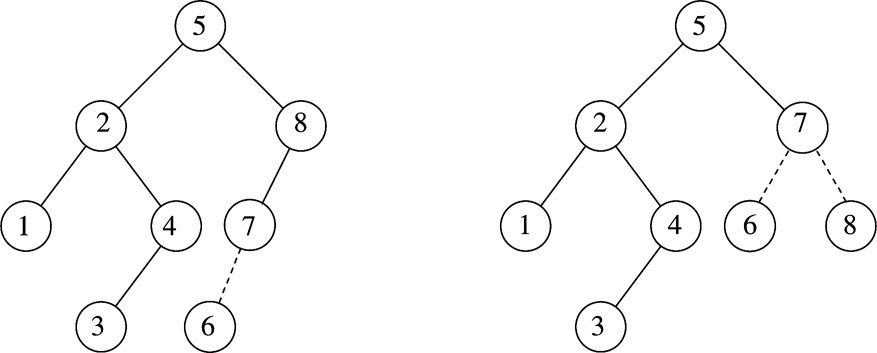
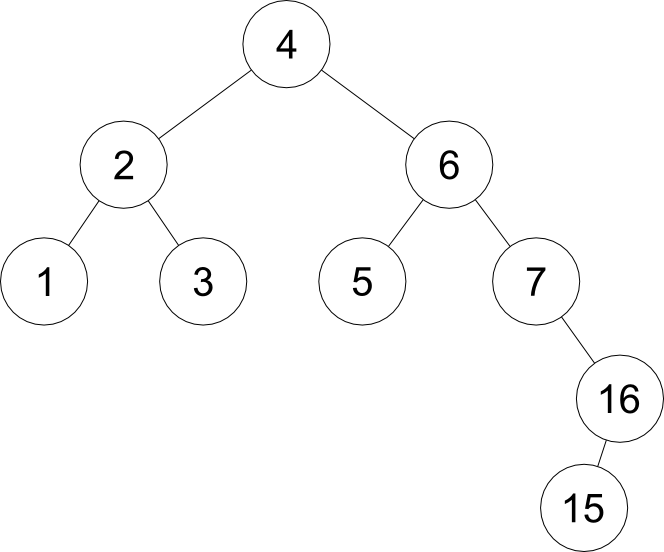
Left-Right case
- Requires double rotation
- Rotation begins at the point where we became out of balance
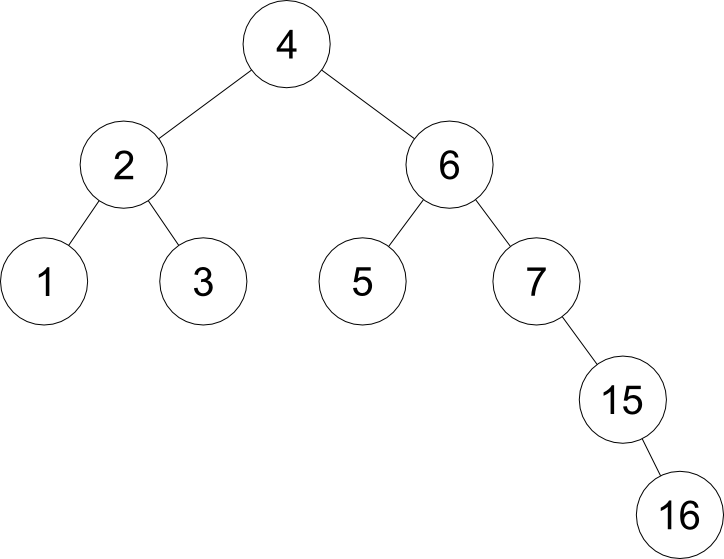
Left-Right case
Left-Right case
Left-Right case
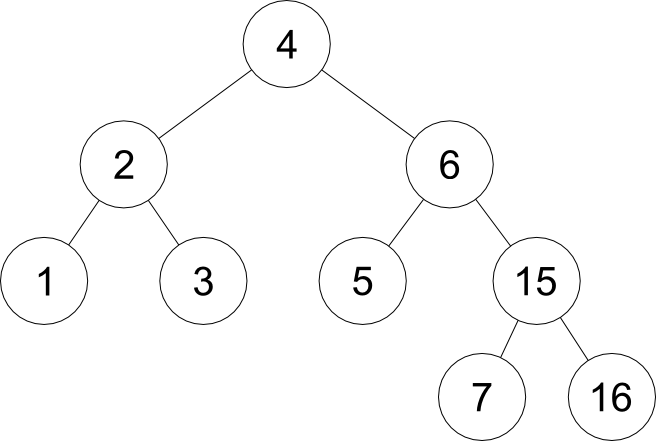
AVL Tree review
- Balance factor
- Each node's balance factor is only allowed to be off by 1 (-1,0,1 are valid).
- Insertion results in 4 cases (reducable to 2).
- Inside case.
- Outside case.
- Only need to balance to the point where the tree went out of balance.
Deleting Nodes
- Begin by doing delete by copy (as mentioned before).
- Check balance factors all the way to the root of the tree.
- May need to rebalance more than once.
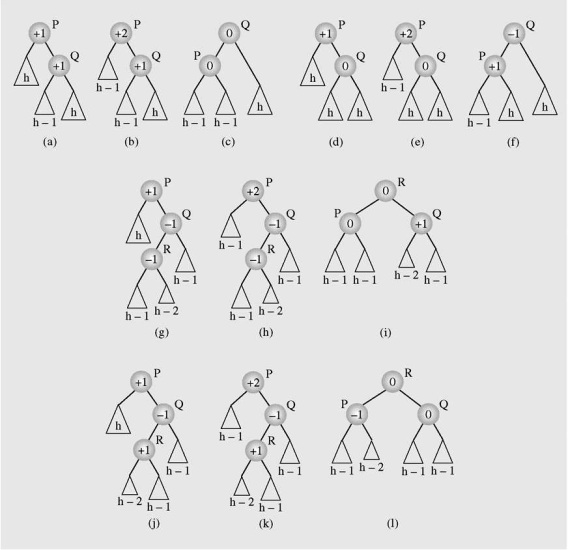
Rebalancing the tree
- When a node is found to be out of balance, one of 4 cases will apply.
- Node is deleted from the lefthand tree, and the right child has a balance factor of +1.
- Node is deleted from the lefthand tree, and the right child has a balance factor of 0.
- Node is deleted from the lefthand tree, the right child has a balance factor of -1, and the left subtree of the right child has a balance factor of -1.
- Node is deleted from the lefthand tree, the right child has a balance factor of -1, and the left subtree of the right child has a balance factor of +1.
Rebalancing the tree
- Node is deleted from the lefthand tree, and the right child has a balance factor of +1.
- Node is deleted from the lefthand tree, and the right child has a balance factor of 0.
- Node is deleted from the lefthand tree, the right child has a balance factor of -1, and the left subtree of the right child has a balance factor of -1.
- Node is deleted from the lefthand tree, the right child has a balance factor of -1, and the left subtree of the right child has a balance factor of +1.
- Node is deleted from the lefthand tree, the right child has a balance factor of -1, and the left subtree of the right child has a balance factor of 0.
Delete AVL Node