Multi-way Trees

Reducing height by increasing width

Nathan Tenney

WSU Tricities

Multi-way trees

• We've considered memory resident data structures up to this point
• If we need to store more information than can be feasibly placed in main memory, what next?
  • Big-oh model breaks down, we can no longer assume that all operations are created equal.
  • Time to access a block on disk $access\_time = seek\_time + latency + transfer\_time$
  • $$40ms + 10ms + 5ms = 55ms$$
  • compared to memory access time, this is 1000 to 1 million time slower
• Need to come up with a structure that would minimize disk accesses

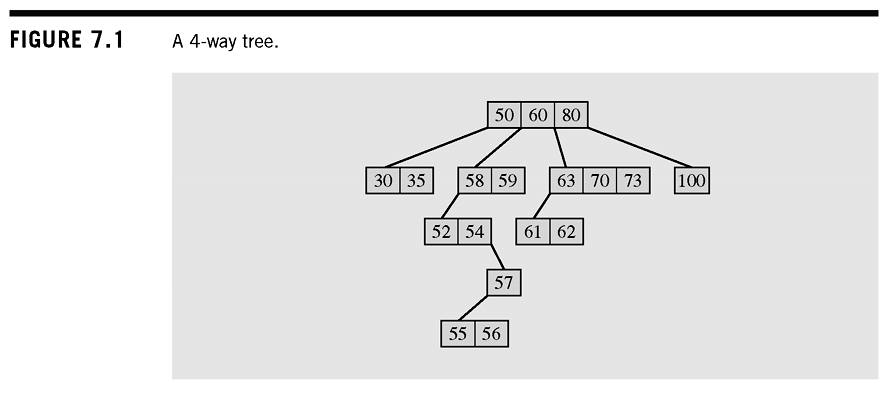
M-ary trees

• Allows M-Way branching
• A perfect binary tree of 31 nodes has 5 levels. while a 5-ary tree of 31 nodes has 3 levels
• Consists of $M-1$ keys and M children
• The height of a complete binary tree is rougly $\log_MN$ compared to $\log_2N$ for a complete binary tree
• Need to ensure that the M-way tree doesn't degenerate into a binary tree

M-ary trees

B-Trees

• Used in programs where most information is stored on Disk (Database programs)
• The size of each node can be made as large as a block on disk
• The number of keys is limited by several factors
  • Organization of Data
  • Key size
  • Size of a block for the given hardware (varies)

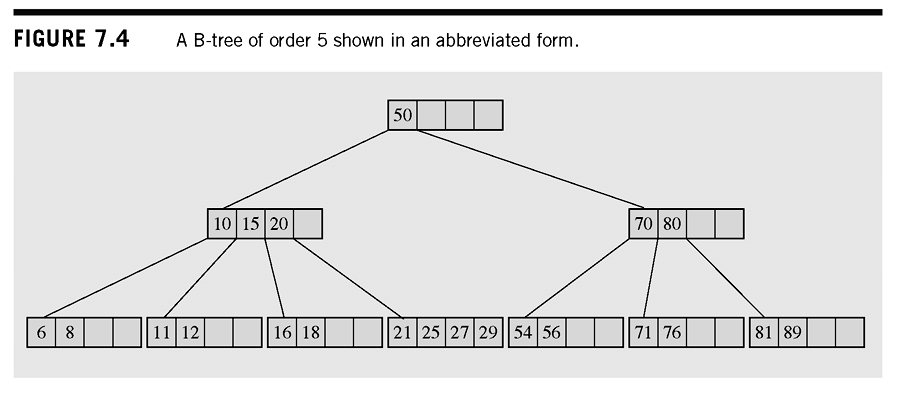
B-Trees

• The properties of a B-Tree are:
  1. The root is either a leaf or has between 2 and M children
  2. Each non-root and non-leaf node holds $k-1$ keys and $k$ pointers to subtrees where $\lceil M/2 \rceil \le k \le M$
  3. Each leaf node holds $k-1$ keys where $\lceil M/2 \rceil \le k \le M$
  4. All leaves are on the same level

B-Trees

• These conditions ensure that:
  • A B-Tree is always at least half full
  • A B-Tree has few levels
  • A B-Tree is perfectly balanced

B-Trees

Worst case

let q be the minimum number of children a node can have ($q = \lceil m/2 \rceil$)

• 1 key in the root
• $2(q-1)$ keys on the second level
• $2q(q-1)$ keys on the third level
• $2q^{2}(q-1)$ keys on the foruth level
• $2q^{h-2}(q-1)$ keys at the leaves
• Total of $1 + (\sum_{i=0}^{h-2}2q^{i})(q-1)$ keys in the tree.

Worst case

$$\sum_{i=0}^{n}q^{i} = \frac{q^{n+1} - 1}{q - 1} \\ \begin{aligned} 1+2(q-1)(\sum_{i=0}^{h-2}q^{i}) &=& 1+1+2(q-1)(\frac{q^{h-1}-1}{q-1}) \\ &=& -1+2q^{h-1} \end{aligned}$$

Worst case

• Relation between number of keys n in any B-Tree and the height is: $n\ge-1+2q^{h-1}$
• Solved for height: $h \le \lfloor \log_{q}\frac{n+1}{2} + 1 \rfloor$
• For a sufficiently large order m, the height is small, even for a large number of nodes
  • m = 200, n = 2,000,000, $h \le 4$

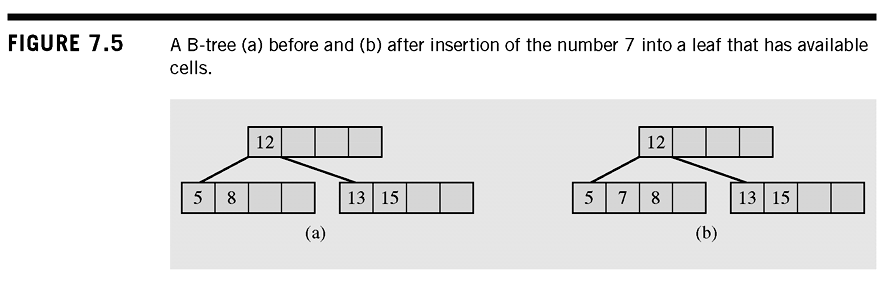
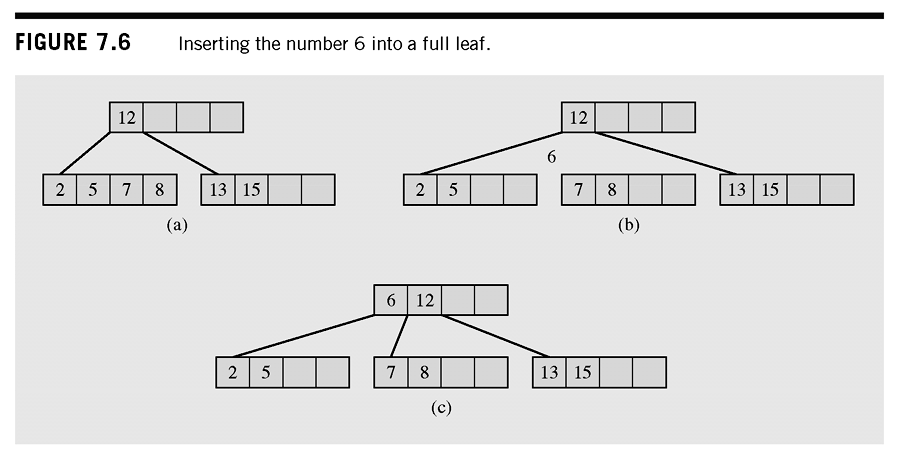
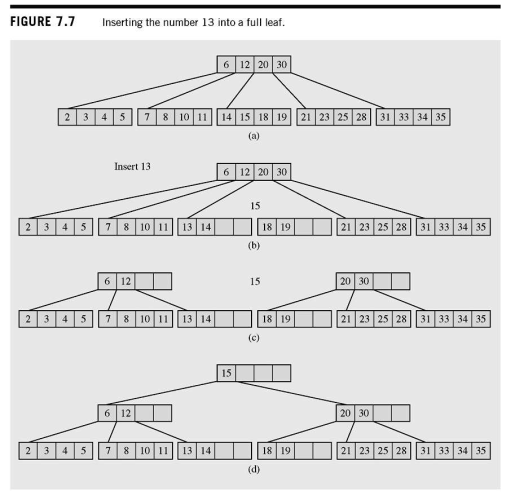
Insertion

1. A key is placed in a leaf that still has some room
2. If the leaf the key should be placed in is full, the leaf is split to create a new leaf. Half of the keys in the full leaf are moved to the new leaf, and the middle key is moved to the parent. If necessary this procedure is repeated to the root
   • Guarantees that each leaf never has less than $\lceil m/2 \rceil$ keys
3. if the root is full, a new root needs to be created, along with a new sibling to the current root.

Insertion

Insertion

Deletion

• In deleting a key, there are 2 cases we need to consider:
  • If the key is in a leaf node
  • If the key is in a non-leaf node
• In the non-leaf case, we'll use a process similar to Delete by Copy

Deletion from a leaf

• Delete key K from leaf node.
  • If after deleting K, the node is at least half full, shift nodes right of K to the left to fill the hole
  • If after deleting K, the number of keys in the leaf is less than $\lceil M/2 \rceil - 1$ we have an underflow

Underflow Condition

• If there is a left or right sibling with the number of keys exceeding $\lceil M/2 \rceil - 1$
  • Redistribute the keys between the current node and the sibling by moving the separator key to the current node, and sending the key between this node and the sibling node to the parent as separator.

Underflow Condition

• If the number of keys in the siblings is $\lceil M/2 \rceil -1$
  • Leaf and a sibling are merged
    • Key from the leaf, the keys from the sibling, and the separator key from the parent are all put into the leaf and the sibling is discarded.
    • If the parent of the leaf is the root, and the root has only one key, all the keys are placed in the leaf, and the root and sibling are deleted. The leaf becomes the new root

Delete from a non-leaf

• The key in question is replaced with the key that is it's immediate predecessor (found only in a leaf)
• The key is deleted from the leaf, which takes us back to the inital step of removing a key from a leaf.

Deletion from B-Tree

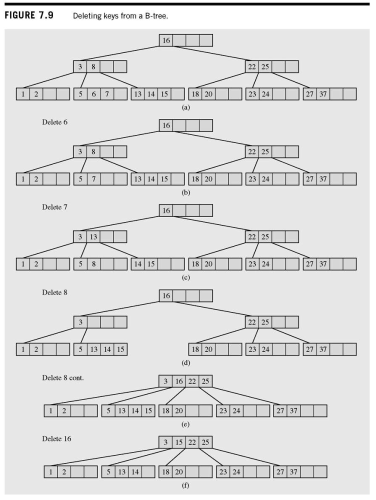
B-Tree sparseness

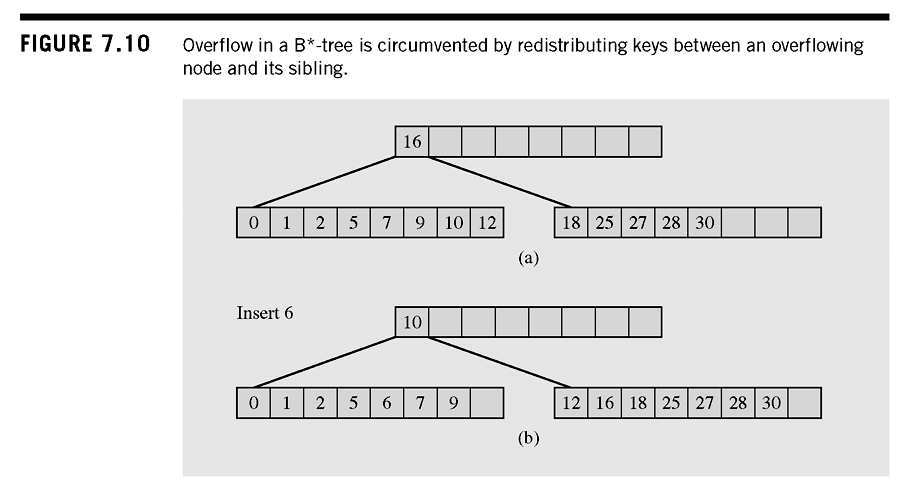
B*-Trees

• Variant on B-Trees
  • Requires that all nodes except the root are $2/3$'s full
  • Splits are delayed by distributing keys between a node and it's siblings.

B*-Tree insertion

General Multi-way Tree Implementation

• Binary Trees and B-Trees have something in common
  • They place limits on the number of children a node may have
• How are binary tree nodes implemented?
• Implementation possiblities for binary and B-Trees?
  • Array based implementation
  • Linked Structure

General Multi-way Tree Implementation

• Linked child list
• Left child, right sibling