Data Compression

Doing More With Less

Nathan Tenney

WSU Tri-Cities

Data Representation

• How is text data represented in a computer?
• What difficulties does this present?
• Can we do better (and what defines 'better')?

Compression Basics

• What is good compression?
  • Assume there are n symbols used to code message
    • Binary code $n = 2$
    • Morse code $n = 3$
  • Assume that all symbols $m_{i}$ in set M have been independantly chosen and have probability of occurrance $P(m_{i})$. Then $P(m_{1}) + ... + P(m_{n}) = 1$

Compression Basics

• The entropy of M is defined as: $L_{ave} = P(m_{1})L(m_{1}) + ... + P(m_{n})L(m_{n})$ where $L(m_{i}) = -log_2(P(m_{i}))$
• $log_b(x) = log_a(x)/log_a(b)$
• $L_{ave}$ gives the best possible average length for a code word when the symbols and their probabilities are known.
• The closer the average length of a code word is to this value, the better the compression algorithm.
• Example: Given a set of 3 symbols with probabilities .25, .25, and .5 repectively, calculate the $L_{ave}$

Compression Basics

• Some restrictions need to be placed on prospective encryption codes:
  • Each code word corresponds to only one symbol
  • Decoding should not require any look ahead
    • After reading each symbol, it should be possible to determine if the end of a string encoding a symbol of the original message has been reached.
    • This is known as the prefix property meaning that no code word is a prefix for another code word.

Compression Basics

• Prefix Property Example:

*Symbol*	*Code 1*	*Code 2*	*Code 3*
A	1	1	11
B	2	22	12
C	12	12	21

Compression Basics

• Restrictions (continued)
  • The length of a code word for a symbol $m_{j}$ should not exceed the length of a less probable code word $m_{i}$
    • If $P(m_{i}) \le P(m_{j})$ then $L(m_{i}) \ge L(m_{j})$
  • In an optimal encoding system, there should not be any unused short code words
    • 01,000,001,100,101 is not optimal. Why?

Compression Basics

• Restrictions (continued)
  • The length of a code word for a symbol $m_{j}$ should not exceed the length of a less probable code word $m_{i}$
    • If $P(m_{i}) \le P(m_{j})$ then $L(m_{i}) \ge L(m_{j})$
  • In an optimal encoding system, there should not be any unused short code words
    • 01,000,001,100,101 is not optimal. Why?
      • 10 and 11 are not used

Compression Basics

• We can use a binary tree to implement a simple compression algorithm.
• Binary code can be represented in a binary tree.
  • 0 indicates you should traverse the left branch
  • 1 indicates you should traverse the right branch
  • characters in our alphabet reside at the leaves

Compression Basics

• Given an alphabet of a,e,i,s,t, along with blank space and newline characters

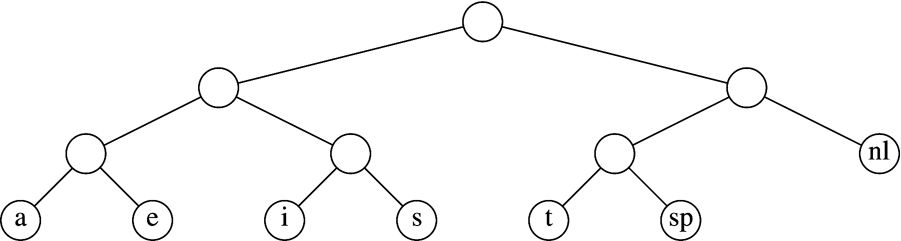
• This Data Structure is known sometimes as a Bitwise Trie

Run Length Encoding

• A run is a sequence of identical characters
• How many runs are in the input aaabba?
• Run length encoding takes adavantage of repeated sequences of characters

Run Length Encoding

• Runs can be encoded by a pair (n,ch) where n is the number of times ch is repeated, and ch is the character.
• What are some potential problems with this?

Run Length Encoding

• To avoid the problem with transmitting runs of numeric characters, n is considered to be an ascii character, and the count of the run is the numeric value of n
• This is inefficent for data that contains large sections of non-repeated characters.
  • How can we make this work better?

Run Length Encoding

• We transmit each run as a tuple.
• Each tuple starts with some character marker
  • A character marker is an infrequently used character that indicates that a run is beginning
  • If the character we are using as the character marker is to be transmitted, we send the character marker twice
• So, to each run is designated by cm,ch,n or %a4

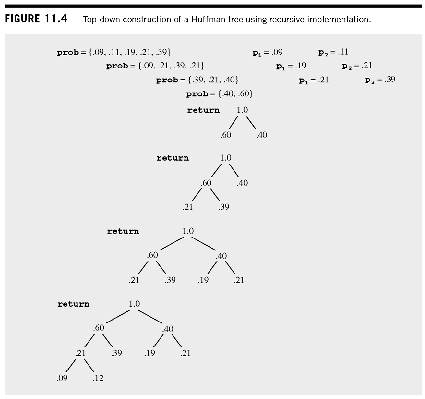
Basic Huffman

• First the language is analyzed, and each character is given a probability based on its typical use in the language
• The letters are put into a list in order of their probabilities, from least to greatest
• Take the two least probable and make them leaves of a new node, whose probabilty is the sum of the probabilities of its children
• Place the new node back in the list in the place of the nodes combined
• Repeat the process until all the characters have been included in the tree

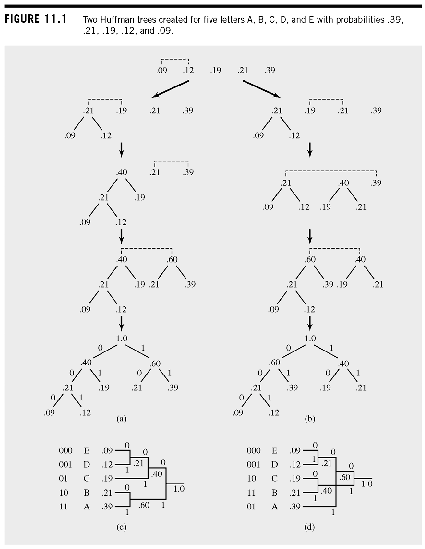
Huffman Example 1

Huffman Example 2

Huffman Example 3

Huffman Efficiency

• Calculate the $L_{ave}$ for the given probabilites (.39,.21,.19,.12,.09)

$L_{ave} = .39(-\frac{log .39}{log 2}) + .21(-\frac{log .21}{log 2}) + .19(-\frac{log .19}{log 2}) + .12(-\frac{log .12}{log 2}) + .09(-\frac{log .09}{log 2})$

• $L(P(m_i))$ is considered to be the length of the code word for the given probability.

• The average length of the Huffman codeword ($L_{huff}$) is defined as:

  $L_{huff} = P(m_1)L(m_1) + ... P(m_i)L(m_i)$ where $L(m_i)$ is the actual length of the encoding for the symbol $m_i$.

Huffman Efficiency

• Calculate the $L_{huff}$ for the given probabilites (.39,.21,.19,.12,.09) and the given encoding lengths (2,2,2,3,3)

$L_{huff} = .39*2 + .21*2 + .19*2 + .12*3 + .09*3$ $diff(L_{ave},L_{huff}) = 1 - \frac{L_{ave}}{L_{huff}}$

Huffman Efficiency

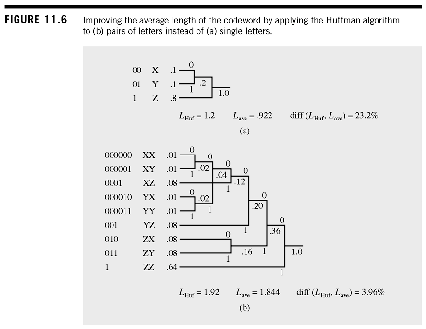
• Calulate the $L_{ave}$ and $L_{huff}$ for (x,y,z) with probabilites (.1,.1,.8)
• Calculate the diff
• Is this very efficient? Can we do better?

Huffman Pairs

Huffman Issues

• Both the sender and receiver need to agree on the huffman tree
• This can be resolved one of three ways
  • Both agree beforehand on the huffman tree and use it
  • Encoder constructs the huffman tree to be used and includes it with the message
  • The decoder constructs the huffman tree during transmission and decoding
• Basic Huffman encoding assumes known probabilities of characters

Lisp Example

(defun queue-length (queue) “Returns as two values the number of elements in the queue and the maximum number of elements the queue can hold.” (check-type queue queue) (let ((length (length (queue-elements queue))) (delta (the fixnum (- (queue-put-ptr queue) (queue-get-ptr queue))))) (declare (fixnum length delta)) ;; The maximum number of elements the queue can hold is ;; (1- LENGTH) because a queue is empty when put-ptr = ;; get-ptr. (values (mod delta length) (the fixnum (1- length)))))

Sibling Property

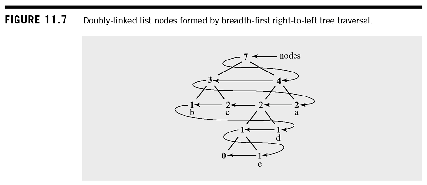
• Assume that each node contains a count variable indicating the frequency that the item has been seen in a message

If each node has a sibling (except the root), and the breadth first right to left traversal generates a list of nodes with non-increasing frequency, it can be proven that a tree adhering to the sibling property is a Huffman tree.

Sibling Property

• Nodes in the tree are organized into blocks made up of nodes with the same size
• The first node in each block is known as the leader of the block

Adaptive Huffman

• Based off the third resolution
• Encoder and decoder build the huffman tree as the message is read
• Entire alphabet is stored in a Zero Node, which starts as the root of the tree
• One of two cases will be true
  • The item to be encoded has not been seen yet in the message
  • The item to be encoded has already been encoded for this message
• Traversal through the tree produces a 0 for each time you go left and a 1 for each time you go right

Adaptive Huffman

• If the item has not been seen before
  • Traverse the tree to the zero node
  • Traverse the zero node looking for the item requested
  • For each item in the zero node that you traverse a 1 is output
  • Once the item in the zero node is reached, a 0 is output

Adaptive Huffman

• If the item has not been seen before (cont.)
  • The found item is removed, and is replaced by the last item in the zero node
  • Two new nodes are created for the tree.
    • One node becomes the sibling of the zero node, It contains the found item, and a count of one
    • The other node becomes the parent of the zero node and the other new node, and it’s count is set to 1

Adaptive Huffman

• The item has already been encoded before
  • Traverse the tree to the leaf that contains the item, outputting the appropriate 0 or 1.
• For either case, we need to update the count stored in the node
• Test the sibling property

Adaptive Huffman

• If the sibling property is violated, the tree must be restructured.
  • Assume that the algorithm is maintaining a doubly linked list of nodes ordered by the breadth first right to left traversal.
  • Starting at the current node P, the block list is traversed forwards to the leader of the block.
  • if the leader of the block is not P’s parent, P is swapped with it.
• Updating of counts continues starting at P’s possibly new root.

Adaptive Huffman Example

• Given an alphabet of a,b,c,d,e,f Encode and decode the message: aafcccbd